In this article, we’re going to do a deep dive into the idea of entropy, one of the most important concepts in information theory, and a critical tool in text analytics. We’ll review how to calculate entropy, some nuances related to measuring entropy in texts, and of course, lots of code along the way.
What is Entropy?
Put simply, entropy is a measure of uncertainty. Imagine picking numbers from a lottery machine. If every ball in the machine had the number 4 written on it, then you would know with 100% certainty that no matter which ball you pick, it would be the number 4. In other words, the uncertainty would be zero, and the entropy would also be zero. As you add more balls, with different numbers, and in different quantities, the uncertainty goes up. And so does the entropy. To use slightly more technical terms, entropy measures the uncertainty in a probability distribution. If you make a random observation of the distribution, entropy tells you how likely you are to be able to guess the outcome ahead of time. With low entropy, it’s very easy to guess (as with the lottery machine that only has 4’s). With high entropy, it’s very difficult.
Although the term “entropy” goes back to the mid-19th century, when it was first used to describe disorder in thermodynamic systems, the term’s history in information theory is more recent. Mathematician Claude Shannon first developed the concept in 1948, in his paper titled A Mathematical Theory of Communication. Shannon was working on how to encode information for transmission (and secrecy!) and entropy was a key idea in understanding how to compress messages without losing any information.
Entropy relates to all kinds of information, but right from the start, Shannon recognized its applicability to language. In his 1951 paper, Prediction and Entropy of Printed English, Shannon used entropy to evaluate the redundancy of a language, and thus its predictability. For our purposes in text analytics, we can use entropy as a way of evaluating the complexity and information content of a text. A document that uses a limited vocabulary, with simple grammatical constructions, is a document with low entropy, because it is relatively predictable.
Consider the sentence “I like red apples, and I like yellow bananas.” If we masked the colors, as in “I like ____ apples, and ____ bananas”, most readers could predict them after a guess or two, especially once they identified the pattern of “I like (color) (fruit).” In this way, we can see that it’s a sentence with low entropy. Compare this to an unusual sentence like “Quixotic chrysanthemums tango beneath stars that smelled of purple.” Here we have rare words in unexpected combinations. If we masked the word “purple”, almost no one would guess it on the first try. By comparison to our first sentence, this one has much higher entropy.
Now that we know a bit about entropy, let’s look at how to calculate it. Formally, entropy is defined for discrete random variable :
where:
- is the probability of occurrence of event ;
- is the number of possible events; and,
- The logarithm is base 2, meaning we’re measuring entropy in bits. (We could measure in other units, but for now let’s stick with bits.)
Let’s see if we can understand what is happening by implementing the formula in Python.
Character Entropy
In our first implementation, we’ll calculate entropy based on characters in a string, using the character-level probability distribution of the string itself as context. We’ll come back later to why the context matters.
First, let’s define a Python function to calculate entropy.
def char_entropy(text: str) -> float: """ Calculates the character-level Shannon entropy of a text, in bits, using probability distribution of characters in the text.
Args: text: str: The input text.
Returns: float: The Shannon entropy of the text. """ # calculate the frequency of each character in the text freqs = Counter(text)
# calculate the entropy using the formula -sum(p * log2(p)) # where p is the probability of each character total_chars = len(text) entropy = 0.0 for freq in freqs.values(): prob = freq / total_chars entropy -= prob * log2(prob)
return entropyNow that we have our function, let’s try it out on a few simple strings.
all_a = "aaaaaa"ab_repeat = "ababab"first_letters = "abcdef"rare_letters = "jkqvxz"
sents = [all_a, ab_repeat, first_letters, rare_letters]
for s in sents: print(f"{s} (entropy: {char_entropy(s)})")
# ---- Output -----# aaaaaa (entropy: 0.0)# ababab (entropy: 1.0)# abcdef (entropy: 2.584962500721156)# jkqvxz (entropy: 2.584962500721156)At the character level, our results show us that the string aaaaaa has an entropy of 0.0, meaning that it has no uncertainty, and thus contains no information. Imagine that you are randomly selecting letters to print, but you’re selecting the from an alphabet that only consists of the letter a. Given that there is only a single outcome (the letter a being selected), we have zero uncertainty and can accurately predict the outcome every time.
By comparison, the string ababab has higher entropy (1.0) because its alphabet consists of two letters, and the probability of drawing each is 50% (we’ll assume a uniform distribution for now). This means that we have an element of uncertainty, because rather than ababab, we might well have ended up with aaabbb or aaabaa and many other combinations. And once we expand the alphabet to six letters, as in abcdef or jkqvxz, the entropy goes up even higher to 2.584.
There is, however, a problem with this approach. We know that in the real world, the alphabet consists of more than one, two, or six letters. The English alphabet has 26 letters, plus lowercase and capital forms, plus punctuation marks. What happens if we take the whole alphabet into consideration?
def char_entropy_with_dist(text: str, prob_dist: dict[str, float], verbose: bool = False) -> float: """ Calculates the Shannon entropy of a text string, given a probability distribution for lowercase letters.
Args: text: The input text string (letters only). prob_dist: A dictionary mapping lowercase letters to their probabilities.
Returns: A dictionary with the entropy and total information content of the text. """ if re.search(r'[^A-Za-z]', text): # validate input print("Error: Input contains non-letter characters") raise ValueError("Input text must contain only letters A-Z or a-z")
text = text.lower() # ensure lowercase
if verbose: print(f"Input text (lowercase): {text} (len: {len(text)})")
entropy = 0 information = 0 for char in text: if char in prob_dist: prob = prob_dist[char] char_info = -np.log2(prob) contribution = prob * char_info entropy = entropy + contribution information = information + char_info
if verbose: print(f"Character: {char}, Probability: {prob:.6f}, Information: {char_info:.6f}, Contribution: {contribution:.6f}")
if verbose: print(f"Final entropy: {entropy}") print(f"Total information: {information}\n") return {"entropy": entropy, "information": information}In our new entropy function, we accept a probability distribution as an argument. The distribution allows us to provide context to the calculation, rather than assuming that the input text includes the entirety of available options. Now, when we calculate entropy of aaaaaa, we can do so knowing that a is just one letter out of 26 in the English alphabet. First, let’s assume that we have a uniform distribution of letter frequency in the alphabet, meaning each character is equally likely to be selected.
uniform_dist = {char: 1/26 for char in 'abcdefghijklmnopqrstuvwxyz'}
print("Uniform alphabet distribution:\n")for s in sents: char_entropy_with_dist(s, uniform_dist, verbose=True)Uniform alphabet distribution:
Input text (lowercase): aaaaaa (len: 6)Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Final entropy: 1.0847168580325597Total information: 28.20263830884655
Input text (lowercase): ababab (len: 6)Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: b, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: b, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: b, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Final entropy: 1.0847168580325597Total information: 28.20263830884655
Input text (lowercase): abcdef (len: 6)Character: a, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: b, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: c, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: d, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: e, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: f, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Final entropy: 1.0847168580325597Total information: 28.20263830884655
Input text (lowercase): jkqvxz (len: 6)Character: j, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: k, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: q, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: v, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: x, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Character: z, Probability: 0.038462, Information: 4.700440, Contribution: 0.180786Final entropy: 1.0847168580325597Total information: 28.20263830884655With a uniform distribution, we see that all of our strings have the same entropy! If each letter is equally likely to be selected, then each string of the same length is equally likely. This makes the uncertainty (or “surprise”) of each outcome the same. Every string still contains some information, given that there are potential outcomes in a six-character string, but no single string is more likely than another.
Before moving on, we should take a moment to break down the formula for entropy, as it contains a few important elements. The entropy is the sum of the weighted information content (aka uncertainty, or surprise) of each character in the string. The information content of a given character is . By intuition, we know that an outcome with a lower probability is more “surprising” and therefore should provide more information than an outcome with higher probability. The logarithm serves two purposes: first, for values between 0 and 1 (that is, all probabilities), it produces larger values for smaller inputs (matching our intuition for greater surprise with smaller probabilities); and second, since the logarithm function is non-linear, very rare events carry more weight than semi-rare events. Finally, we invert the sign because the logarithm of a value between 0 and 1 is always negative, and we want our information measure to be positive. With this, we can say that the information content , measured on scale (usually 2, for bits), of a value is:
Going back to our uniform distribution, we observed that every letter had the same information content and contribution to entropy. But, we know that’s not how language works. In every language, certain letters are used more frequently than others, because langauges have patterns, and rules that dictate spelling. In English for example, we know that q is a low frequency letter (hence the high score in Scrabble!) and e is very common. So what happens if we use a more realistic distribution, based on actual observations of the English language? Let’s find out, using this handy real-world distribution provided by the University of Notre Dame.
observed_dist = { 'a': 0.084966, 'b': 0.020720, 'c': 0.045388, 'd': 0.033844, 'e': 0.111607, 'f': 0.018121, 'g': 0.024705, 'h': 0.030034, 'i': 0.075448, 'j': 0.001965, 'k': 0.011016, 'l': 0.054893, 'm': 0.030129, 'n': 0.066544, 'o': 0.071635, 'p': 0.031671, 'q': 0.001962, 'r': 0.075809, 's': 0.057351, 't': 0.069509, 'u': 0.036308, 'v': 0.010074, 'w': 0.012899, 'x': 0.002902, 'y': 0.017779, 'z': 0.002722}
print("\nObserved distribution:")for s in sents: char_entropy_with_dist(s, observed_dist, verbose=True)Observed distribution:Input text (lowercase): aaaaaa (len: 6)Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Final entropy: 1.8133293544228715Total information: 21.341823251922786
Input text (lowercase): ababab (len: 6)Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: b, Probability: 0.020720, Information: 5.592832, Contribution: 0.115883Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: b, Probability: 0.020720, Information: 5.592832, Contribution: 0.115883Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: b, Probability: 0.020720, Information: 5.592832, Contribution: 0.115883Final entropy: 1.2543151259398315Total information: 27.449408186212164
Input text (lowercase): abcdef (len: 6)Character: a, Probability: 0.084966, Information: 3.556971, Contribution: 0.302222Character: b, Probability: 0.020720, Information: 5.592832, Contribution: 0.115883Character: c, Probability: 0.045388, Information: 4.461545, Contribution: 0.202501Character: d, Probability: 0.033844, Information: 4.884956, Contribution: 0.165326Character: e, Probability: 0.111607, Information: 3.163501, Contribution: 0.353069Character: f, Probability: 0.018121, Information: 5.786194, Contribution: 0.104852Final entropy: 1.2438525366833209Total information: 27.44599829714204
Input text (lowercase): jkqvxz (len: 6)Character: j, Probability: 0.001965, Information: 8.991255, Contribution: 0.017668Character: k, Probability: 0.011016, Information: 6.504256, Contribution: 0.071651Character: q, Probability: 0.001962, Information: 8.993459, Contribution: 0.017645Character: v, Probability: 0.010074, Information: 6.633220, Contribution: 0.066823Character: x, Probability: 0.002902, Information: 8.428737, Contribution: 0.024460Character: z, Probability: 0.002722, Information: 8.521117, Contribution: 0.023194Final entropy: 0.22144159306730116Total information: 48.07204347721594As you can see, the distribution makes a huge difference in the entropy of our strings. Now, instead of them all being the same (as with the uniform distribution), each string has a different entropy. Counterintuitively though, we see that the string aaaaaa actually has the highest entropy, even though a is the second most common letter, and thus contains very little information. Why is this?
If we look back at our entropy formula, we can substitute for to see how information content relates to entropy more clearly:
As we can see, the entropy is not just the sum of information in the string, but the weighted sum, where the information content of each character is weighted by its probability. In other words, very high probability letters like a and e have greater weight than low probability letters like q or z.
At this point, we should clarify what the entropy of a string really means. Entropy is a measure of the average information across all events in a probability distribution. It answers the question, “if I draw from this distribution, on average, how much information should I expect to get out?” So, if we calculate the entropy of a string, what we’re really doing is saying something about that string’s relationship to the overall distribution, rather than something about the string itself.
This raises an important question: in text analytics, should we be measuring the entropy of a string at all? Isn’t the total information content more important? Reasonable minds could argue this point, and different use cases probably prefer different calculations; however, it’s worth noting that the two measurements, though related, tell us something different. The entropy of a text is primarily a question of uncertainty. On average, a text with high entropy is likely to have high information content. Total information though is a function of length, and of information efficiency (how much information, on average, do we pack into each symbol in a text.) It’s a nuanced difference, but meaningful.
As an aside, but beyond the scope of this article, we should acknowledge that our model still doesn’t quite match the real world. Just as we know that real alphabets have non-uniform probability distributions for letter frequency, we also know that each letter is not independent of the last. In our calculations thus far, we have assumed independence. In reality, the probability of each letter should change based off previously observed letters. For example, we know that in English the letter q is very likely to be followed by the letter u, meaning that we should use a different probability for u in that setting than its independent frequency. This type of dependency is often modeled using tools like Markov chains or n-grams, which take into account the probabilities of sequences rather than isolated events. But, that is a discussion for another day.
Just to drive the point home, let’s plot the information content of each letter from each distribution.
def plot_letter_information(distributions: dict | list[dict], labels: list[str] = None, title: str = "Information Content of Letters") -> None: """ Plot the information content of letters given one or more probability distributions.
Args: distributions: Single dictionary or list of dictionaries mapping letters to probabilities labels: List of labels for each distribution (only used if multiple distributions provided) title: Title for the plot """ if isinstance(distributions, dict): distributions = [distributions] labels = ['Distribution'] elif labels is None: labels = [f'Distribution {i+1}' for i in range(len(distributions))]
plt.figure(figsize=(12, 6))
width = 0.8 / len(distributions)
for i, dist in enumerate(distributions): letters = list(dist.keys()) probs = list(dist.values()) info_content = [-log2(p) for p in probs]
x = np.arange(len(letters)) offset = width * (i - (len(distributions)-1)/2)
plt.bar(x + offset, info_content, width, label=labels[i], alpha=0.7)
plt.title(title) plt.xlabel("Letter") plt.ylabel("Information Content (bits)") plt.xticks(range(len(letters)), letters)
if len(distributions) > 1: plt.legend()
ymax = max(max(-log2(p) for p in dist.values()) for dist in distributions) plt.ylim(0, ymax * 1.1)
plt.show()
plot_letter_information( [observed_dist, uniform_dist], labels=["Observed distribution", "Uniform distribution"], title="Information content of English letters")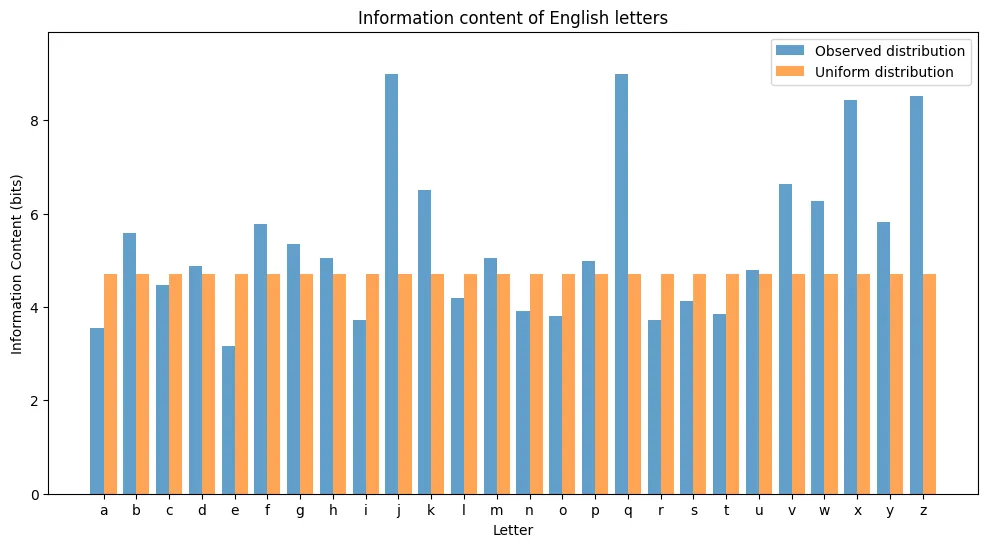
Here, we can clearly see that in the observed distribution (the one drawn from actual English texts), certain letters have far more information content than others. This shows us how important the probability distribution is to the entropy of a text, and the information content of its constituent parts.
And speaking of probabilities and information content, it’s worth taking a look at how the former affects the latter. We can do so by plotting our observed distribution frequencies against the information content for each letter.
def plot_information_vs_probability(dist: dict) -> None: letters = list(dist.keys()) freqs = np.array(list(dist.values())) info_content = -np.log2(freqs)
plt.figure(figsize=(10, 6)) sns.scatterplot(x=freqs, y=info_content, color='b', alpha=0.6)
for i, (letter, x, y) in enumerate(zip(letters, freqs, info_content)): offset = 10 if i % 2 == 0 else -15 plt.annotate(letter, (x, y), xytext=(0, offset), textcoords='offset points', fontsize=10, ha='center')
plt.xlabel("Probability") plt.ylabel("Information Content (bits)") plt.title("Information Content vs. Probability of English Letters")
plt.ylim(bottom=0, top=max(info_content) * 1.1) sns.despine() plt.show()
plot_information_vs_probability(observed_dist)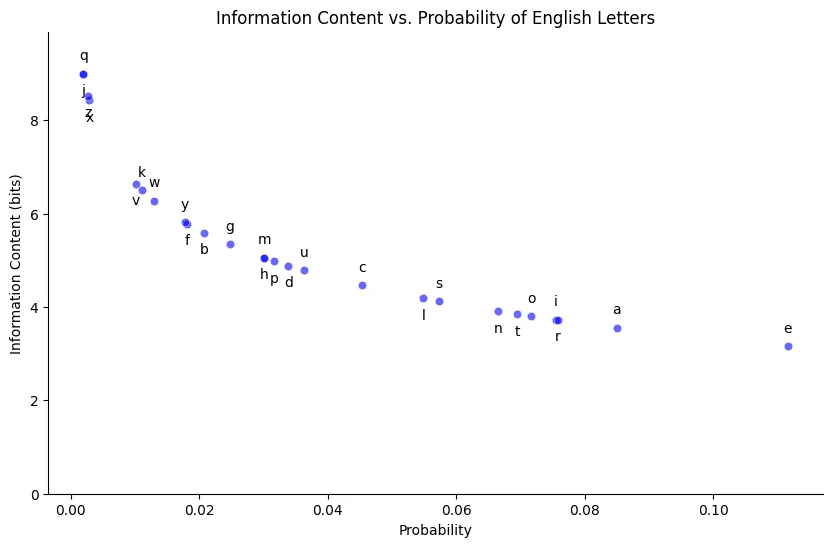
The above plot makes it clear that as probability goes up, information content goes down. This is of course exactly what we expect, given that information content is calculated as , meaning it has a negative logarithmic slope.
What About Words?
Thus far we have been talking about entropy in the context of characters. Although useful for illustrative purposes, or to understand probability distributions within an alphabet, character-based entropy isn’t particularly interesting in most text analytics applications. In general, our main concern isn’t with the information contained in letters, but the information in words.
We know that entropy is calculated as the sum of weighted information content for each observation drawn from a random variable. In the context of character-based entropy, the range of possible observations was the lowercase alphabet, and the probability distribution was the frequency those letters appear in a language using that alphabet. Now, in the context of word-based entropy, each observation is a single word, drawn from a range that consists of all words in a given vocabulary, and the frequency of those words as they appear in some corpus of texts. Ideally, it would be nice to have the entropy of an entire language, but given how languages change over time, and the impracticality of observing every use of a word in any context, written or spoken, anywhere, over all of time, we have to settle for vocabularies and frequencies as defined by a particular collection of texts.
So, where do we get these vocabularies and probability distributions? Well, to start, we could make our own. Consider the following simple sentences.
fruit_sentences = [ "I like red apples, and I like yellow bananas.", "I eat apples, oranges, or bananas, daily.", "I like bananas more than red apples or oranges.", "I sometimes pick my own apples and oranges.", "My dog Rex likes apples and bananas."]fruit_text = " ".join(fruit_sentences).lower()
# remove punctuationfruit_text = re.sub(r'[^\w\s]', '', fruit_text)
# build vocabulary and frequency distributionfruit_freqs = Counter(fruit_text.split())
# calculate probabilitiestotal_words = sum(fruit_freqs.values())fruit_probs = {word: freq / total_words for word, freq in fruit_freqs.items()}
fruit_df = pd.DataFrame({ "word": list(fruit_freqs.keys()), "freq": list(fruit_freqs.values()), "prob": list(fruit_probs.values()), "info": [-np.log2(p) for p in fruit_probs.values()], "entropy_contribution": [p * -np.log2(p) for p in fruit_probs.values()]}).sort_values("freq", ascending=False).reset_index(drop=True)
fruit_df| word | freq | prob | info | entropy_contribution |
|---|---|---|---|---|
| i | 5 | 0.125 | 3.000000 | 0.375000 |
| apples | 5 | 0.125 | 3.000000 | 0.375000 |
| bananas | 4 | 0.100 | 3.321928 | 0.332193 |
| and | 3 | 0.075 | 3.736966 | 0.280272 |
| oranges | 3 | 0.075 | 3.736966 | 0.280272 |
| like | 3 | 0.075 | 3.736966 | 0.280272 |
| red | 2 | 0.050 | 4.321928 | 0.216096 |
| or | 2 | 0.050 | 4.321928 | 0.216096 |
| my | 2 | 0.050 | 4.321928 | 0.216096 |
| pick | 1 | 0.025 | 5.321928 | 0.133048 |
| rex | 1 | 0.025 | 5.321928 | 0.133048 |
| dog | 1 | 0.025 | 5.321928 | 0.133048 |
| own | 1 | 0.025 | 5.321928 | 0.133048 |
| daily | 1 | 0.025 | 5.321928 | 0.133048 |
| sometimes | 1 | 0.025 | 5.321928 | 0.133048 |
| than | 1 | 0.025 | 5.321928 | 0.133048 |
| more | 1 | 0.025 | 5.321928 | 0.133048 |
| eat | 1 | 0.025 | 5.321928 | 0.133048 |
| yellow | 1 | 0.025 | 5.321928 | 0.133048 |
| likes | 1 | 0.025 | 5.321928 | 0.133048 |
In this corpus of five sentences, our vocabulary has 20 words, with words like I, apples, and bananas having high probability. If we randomly draw a word from this corpus, we wouldn’t be particularly surprised if we drew apples, because it is high frequency. So, in the context of this corpus, apples has relatively low information content. By comparison, the word dog only occurs a single time, and thus has much higher information content. Let’s use the same methodology as before to calculate entropy for this corpus.
def calculate_corpus_entropy( corpus: list[str], prob_func: Optional[Callable] = None) -> dict: """ Calculate entropy and information metrics for a corpus of text.
Args: corpus: A list of strings representing the texts to analyze prob_func: A function to calculate the probability of a word given its frequency. If None, the probability is calculated as the freq / total_words.
Returns: dict containing: - entropy: The total entropy of the corpus - information_content: The total information content - word_data: DataFrame with per-word statistics """ # join all texts and convert to lowercase full_text = " ".join(corpus).lower()
# remove punctuation and split into words words = re.sub(r'[^\w\s]', '', full_text).split()
# calculate frequencies freqs = Counter(words) total_words = sum(freqs.values())
# calculate metrics for each word word_data = [] total_entropy = 0 total_information = 0
for word, freq in freqs.items(): prob = prob_func(word) if prob_func else freq / total_words information = -np.log2(prob) # information content in bits entropy_contribution = prob * information
word_data.append({ 'word': word, 'frequency': freq, 'probability': prob, 'information': information, 'entropy_contribution': entropy_contribution })
total_entropy += entropy_contribution total_information += information
word_df = pd.DataFrame(word_data).sort_values('frequency', ascending=False).reset_index(drop=True)
return { 'entropy': total_entropy, 'information_content': total_information, 'total_words': total_words, 'total_vocab': len(freqs), 'word_data': word_df }
fruit_data = calculate_corpus_entropy(fruit_sentences)
print(f"Total entropy: {fruit_data['entropy']:.4f}")print(f"Total information content: {fruit_data['information_content']:.4f}")print(f"Total words: {fruit_data['total_words']}")print(f"Total vocabulary: {fruit_data['total_vocab']}")
fruit_data['word_data']Total entropy: 4.0348Total information content: 92.0398Total words: 40Total vocabulary: 20| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| i | 5 | 0.125 | 3.000000 | 0.375000 |
| apples | 5 | 0.125 | 3.000000 | 0.375000 |
| bananas | 4 | 0.100 | 3.321928 | 0.332193 |
| and | 3 | 0.075 | 3.736966 | 0.280272 |
| oranges | 3 | 0.075 | 3.736966 | 0.280272 |
| like | 3 | 0.075 | 3.736966 | 0.280272 |
| red | 2 | 0.050 | 4.321928 | 0.216096 |
| or | 2 | 0.050 | 4.321928 | 0.216096 |
| my | 2 | 0.050 | 4.321928 | 0.216096 |
| pick | 1 | 0.025 | 5.321928 | 0.133048 |
| rex | 1 | 0.025 | 5.321928 | 0.133048 |
| dog | 1 | 0.025 | 5.321928 | 0.133048 |
| own | 1 | 0.025 | 5.321928 | 0.133048 |
| daily | 1 | 0.025 | 5.321928 | 0.133048 |
| sometimes | 1 | 0.025 | 5.321928 | 0.133048 |
| than | 1 | 0.025 | 5.321928 | 0.133048 |
| more | 1 | 0.025 | 5.321928 | 0.133048 |
| eat | 1 | 0.025 | 5.321928 | 0.133048 |
| yellow | 1 | 0.025 | 5.321928 | 0.133048 |
| likes | 1 | 0.025 | 5.321928 | 0.133048 |
Here, we see that our corpus of texts, fruit_sentences, has an entropy of and total information content of . As expected, the rare words like dog, rex, and yellow contribute more information content, but since entropy contributions are weighted by frequency, high probability words like apples and bananas end up contributing more total entropy.
Of course, this is a very small corpus, with a very small vocabulary. Let’s try calculating entropy for a corpus with a much larger vocabulary. To do this, let’s take a look at the vocabulary in Crime and Punishment. After downloading the text, we’ll run it through the same function
def read_text_from_url(url: str, encoding: str = 'utf-8') -> str: """ Reads text content from a URL with specified encoding.
Args: url (str): The URL of the text file to read encoding (str, optional): The encoding to use when reading the text. Defaults to 'utf-8'.
Returns: str: The text content from the URL
Raises: requests.RequestException: If the request fails """ try: response = requests.get(url) response.raise_for_status() # Raise an exception for bad status codes response.encoding = encoding # Set the encoding return response.text except requests.RequestException as e: print(f"Error fetching text from URL: {e}") raise
# download textcrime_url = "https://www.gutenberg.org/ebooks/2554.txt.utf-8"crime_text = read_text_from_url(crime_url)
# trim metadatastart_marker = "*** START OF THE PROJECT GUTENBERG EBOOK CRIME AND PUNISHMENT ***"crime_text = crime_text[crime_text.find(start_marker) + len(start_marker):].strip()
# extract single chaptercrime_chp_1 = crime_text[crime_text.find("CHAPTER I"):crime_text.find("CHAPTER II")].strip()Before diving into the whole text, let’s try out our methodology on a single chapter. This will let us compare calculations from a single chapter to that for the full text, and see how probability distributions affect information content and entropy for particular words.
crime_chp_1_data = calculate_corpus_entropy([crime_chp_1])
print(f"Total entropy: {crime_chp_1_data['entropy']:.4f}")print(f"Total information content: {crime_chp_1_data['information_content']:.4f}")print(f"Total words: {crime_chp_1_data['total_words']}")print(f"Total vocabulary: {crime_chp_1_data['total_vocab']}")
print("\nWord data:")crime_chp_1_data['word_data'].head(20)Total entropy: 8.3847Total information content: 11127.1207Total words: 3328Total vocabulary: 1013| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| the | 186 | 0.055889 | 4.161281 | 0.232572 |
| and | 114 | 0.034255 | 4.867550 | 0.166737 |
| a | 107 | 0.032151 | 4.958973 | 0.159438 |
| he | 100 | 0.030048 | 5.056584 | 0.151941 |
| in | 82 | 0.024639 | 5.342888 | 0.131646 |
| of | 77 | 0.023137 | 5.433653 | 0.125719 |
| to | 69 | 0.020733 | 5.591915 | 0.115938 |
| was | 60 | 0.018029 | 5.793549 | 0.104451 |
| it | 43 | 0.012921 | 6.274175 | 0.081067 |
| his | 39 | 0.011719 | 6.415037 | 0.075176 |
| that | 38 | 0.011418 | 6.452512 | 0.073677 |
| at | 34 | 0.010216 | 6.612977 | 0.067560 |
| i | 32 | 0.009615 | 6.700440 | 0.064427 |
| as | 30 | 0.009014 | 6.793549 | 0.061240 |
| had | 30 | 0.009014 | 6.793549 | 0.061240 |
| on | 29 | 0.008714 | 6.842459 | 0.059625 |
| with | 29 | 0.008714 | 6.842459 | 0.059625 |
| but | 26 | 0.007812 | 7.000000 | 0.054688 |
| for | 24 | 0.007212 | 7.115477 | 0.051314 |
| all | 24 | 0.007212 | 7.115477 | 0.051314 |
Looking at the first chapter only, we get a total entropy of . Remember, this is the entropy of the probability distribution seen in this chapter only. We’ll see in a moment how it changes when we look at the full text. But already we can see it’s much higher than the entropy of our fruit sentences, because the vocabulary is much bigger and there is thus more uncertainty of which word will come out when we make a random selection.
It’s worth pointing out as well that, unsurprisingly, the most frequent words are so-called stopwords, that is, filler words that are important to the structure of a language, but not particularly original or unique. Let’s try sorting by information content.
crime_chp_1_data['word_data'].sort_values("information", ascending=False).head(20)| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| waking | 1 | 0.000300 | 11.700440 | 0.003516 |
| bustle | 1 | 0.000300 | 11.700440 | 0.003516 |
| insufferable | 1 | 0.000300 | 11.700440 | 0.003516 |
| overwrought | 1 | 0.000300 | 11.700440 | 0.003516 |
| learned | 1 | 0.000300 | 11.700440 | 0.003516 |
| lying | 1 | 0.000300 | 11.700440 | 0.003516 |
| together | 1 | 0.000300 | 11.700440 | 0.003516 |
| den | 1 | 0.000300 | 11.700440 | 0.003516 |
| jack | 1 | 0.000300 | 11.700440 | 0.003516 |
| giantkiller | 1 | 0.000300 | 11.700440 | 0.003516 |
| fantasy | 1 | 0.000300 | 11.700440 | 0.003516 |
| amuse | 1 | 0.000300 | 11.700440 | 0.003516 |
| myself | 1 | 0.000300 | 11.700440 | 0.003516 |
| maybe | 1 | 0.000300 | 11.700440 | 0.003516 |
| airlessness | 1 | 0.000300 | 11.700440 | 0.003516 |
| plaster | 1 | 0.000300 | 11.700440 | 0.003516 |
| particularly | 1 | 0.000300 | 11.700440 | 0.003516 |
| scaffolding | 1 | 0.000300 | 11.700440 | 0.003516 |
| bricks | 1 | 0.000300 | 11.700440 | 0.003516 |
| unable | 1 | 0.000300 | 11.700440 | 0.003516 |
Here we see some more interesting words, like giantkiller, and fantasy. These words are very low probability, and thus have very high information content. Looking only at the first chapter, we can see that any word that appeared a single time had an information content of 11.700. We’ll see how that changes with a larger vocabulary shortly.
Now, let’s turn to the full text of Crime and Punishment and see how our numbers change, given the much larger vocabulary, and thus a different probability distribution.
crime_data = calculate_corpus_entropy([crime_text])
print(f"Total entropy: {crime_data['entropy']:.4f}")print(f"Total information content: {crime_data['information_content']:.4f}")print(f"Total words: {crime_data['total_words']}")print(f"Total vocabulary: {crime_data['total_vocab']}")
print("\nWord data:")crime_data['word_data'].head(20)Total entropy: 9.3700Total information content: 174062.3333Total words: 206390Total vocabulary: 10800| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| the | 7976 | 0.038645 | 4.693564 | 0.181384 |
| and | 6968 | 0.033761 | 4.888485 | 0.165042 |
| to | 5342 | 0.025883 | 5.271849 | 0.136451 |
| he | 4652 | 0.022540 | 5.471378 | 0.123324 |
| a | 4622 | 0.022394 | 5.480712 | 0.122738 |
| i | 3936 | 0.019071 | 5.712499 | 0.108941 |
| of | 3921 | 0.018998 | 5.718008 | 0.108631 |
| you | 3873 | 0.018765 | 5.735778 | 0.107634 |
| in | 3242 | 0.015708 | 5.992345 | 0.094129 |
| it | 2983 | 0.014453 | 6.112465 | 0.088345 |
| that | 2915 | 0.014124 | 6.145733 | 0.086801 |
| was | 2821 | 0.013668 | 6.193023 | 0.084648 |
| his | 2113 | 0.010238 | 6.609936 | 0.067672 |
| at | 2075 | 0.010054 | 6.636118 | 0.066718 |
| her | 1822 | 0.008828 | 6.823706 | 0.060239 |
| but | 1784 | 0.008644 | 6.854114 | 0.059246 |
| not | 1771 | 0.008581 | 6.864665 | 0.058905 |
| with | 1751 | 0.008484 | 6.881050 | 0.058378 |
| for | 1671 | 0.008096 | 6.948518 | 0.056257 |
| she | 1626 | 0.007878 | 6.987902 | 0.055053 |
Looking at the full text, our entropy has gone up a bit to , but not nearly as much as the vocabulary, which went from in the first chapter alone, to roughly ten times as much at in the full text. So why didn’t the entropy go up a lot more? The answer lies, at least in part, in the most frequent words. You’ll note that the top words in the full text, as in the first chapter alone, are still all stop words. In fact, the top two words, the and and are the same in both cases! Even though the full text has many more rare words, since entropy contributions are weighted by probability of a word, the stop words still have the most influence.
Speaking of the rare words, let’s see how the information content changed for a few words from the first chapter, compared to the full text.
crime_data['word_data'].sort_values("information", ascending=False).head(20)| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| newsletter | 1 | 0.000005 | 17.655014 | 0.000086 |
| punishing | 1 | 0.000005 | 17.655014 | 0.000086 |
| person_ | 1 | 0.000005 | 17.655014 | 0.000086 |
| peaceably | 1 | 0.000005 | 17.655014 | 0.000086 |
| errors | 1 | 0.000005 | 17.655014 | 0.000086 |
| lettres_ | 1 | 0.000005 | 17.655014 | 0.000086 |
| peaceful | 1 | 0.000005 | 17.655014 | 0.000086 |
| despite | 1 | 0.000005 | 17.655014 | 0.000086 |
| dame | 1 | 0.000005 | 17.655014 | 0.000086 |
| are | 1 | 0.000005 | 17.655014 | 0.000086 |
| appropriately | 1 | 0.000005 | 17.655014 | 0.000086 |
| gold | 1 | 0.000005 | 17.655014 | 0.000086 |
| novelreading | 1 | 0.000005 | 17.655014 | 0.000086 |
| directress | 1 | 0.000005 | 17.655014 | 0.000086 |
| maid | 1 | 0.000005 | 17.655014 | 0.000086 |
| laundry | 1 | 0.000005 | 17.655014 | 0.000086 |
| novels | 1 | 0.000005 | 17.655014 | 0.000086 |
| coughcough | 1 | 0.000005 | 17.655014 | 0.000086 |
| cleverer | 1 | 0.000005 | 17.655014 | 0.000086 |
| epilogue | 1 | 0.000005 | 17.655014 | 0.000086 |
Recall that when we looked at the first chapter alone, words that appeared a single time had information content of . Now, words with a single appearance have an information content of ! In the context of the full text, with the vastly larger vocabulary, single appearance words carry more information, as their probability went down significantly. For comparison, let’s look at the words giantkiller and fantasy, which we saw in the first chapter.
words_of_interest = ["giantkiller", "fantasy"]
print("Interesting word values from chapter 1:")chp_1_words = ( crime_chp_1_data['word_data'][crime_chp_1_data['word_data']['word'] .isin(words_of_interest)] .sort_values("word"))display(chp_1_words)
print("\nInteresting word values from full text:")full_text_words = ( crime_data['word_data'][crime_data['word_data']['word'] .isin(words_of_interest)] .sort_values("word"))display(full_text_words)Interesting word values from chapter 1:
| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| fantasy | 1 | 0.0003 | 11.70044 | 0.003516 |
| giantkiller | 1 | 0.0003 | 11.70044 | 0.003516 |
Interesting word values from full text:
| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| fantasy | 4 | 0.000019 | 15.655014 | 0.000303 |
| giantkiller | 1 | 0.000005 | 17.655014 | 0.000086 |
Here, we see that giantkiller was never used again through the rest of the text, so its probability went down, and its information content therefore went up. By comparison, fantasy appeared several more times. It’s probability still went down in the context of the full text, but not by as much as giantkiller, so it’s information content did not rise as much.
More Realistic Vocabularies
Until now, we have been building our own vocabularies based on relatively small corpora. Crime and Punishment might be a long book, with a huge vocabulary, but the probability distribution in that vocabulary is hardly representative of the language as a whole. Thankfully, libraries like spaCy have already done the hard work of calculating probabilities of words.
spaCy tokens each have an attribute prob, which provides the smoothed log probability estimate of a word (or technically, of its lexeme). The smoothed log probability is drawn from a probability distribution in a three billion word corpus (and then smoothed in order to avoid zero-counts of words that don’t appear in the corpus.) This means that the probabilities are much more representative of the language as a whole, rather than probabilities in the context of our text alone. Let’s update our function to use these probabilities.
def get_spacy_probability(word: str, nlp: spacy.Language) -> float: """ Get the probability of a word in the spaCy language model.
Args: word (string): The word to get the probability for nlp (spacy.Language): The spaCy language model
Returns: The probability of the word (float) """ # ensure word is in vocab _ = nlp.vocab[word]
# spacy prob attribute is actually a natural logarithm of the probability ln_prob = nlp.vocab[word].prob
# convert ln probability back to probability using e^x prob = np.exp(ln_prob)
return prob
# load language modelnlp = spacy.load("en_core_web_md")
# in order to look up the probability, we need to load the lookup tablelookups = load_lookups("en", ["lexeme_prob"])nlp.vocab.lookups.add_table("lexeme_prob", lookups.get_table("lexeme_prob"))print("probabilities loaded...")
sample_probs = ["the", "and", "a", "fantasy", "giantkiller"]
for word in sample_probs: prob = get_spacy_probability(word, nlp) print(f"{word} ({prob:.6f})")the (0.029341)and (0.016357)a (0.019648)fantasy (0.000027)giantkiller (0.000000)crime_data_spacy = calculate_corpus_entropy( [crime_text], prob_func=lambda word: get_spacy_probability(word, nlp))
print(f"Total entropy: {crime_data_spacy['entropy']:.4f}")print(f"Total information content: {crime_data_spacy['information_content']:.4f}")
print("\nWord data:")crime_data_spacy['word_data'].head(20)Total entropy: 5.7979Total information content: 214857.3604| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| the | 7976 | 0.029341 | 5.090934 | 0.149374 |
| and | 6968 | 0.016357 | 5.933961 | 0.097061 |
| to | 5342 | 0.021152 | 5.563063 | 0.117670 |
| he | 4652 | 0.002653 | 8.557930 | 0.022708 |
| a | 4622 | 0.019648 | 5.669486 | 0.111393 |
| i | 3936 | 0.001245 | 9.649857 | 0.012012 |
| of | 3921 | 0.013900 | 6.168782 | 0.085745 |
| you | 3873 | 0.012603 | 6.310047 | 0.079528 |
| in | 3242 | 0.009862 | 6.663912 | 0.065719 |
| it | 2983 | 0.012425 | 6.330618 | 0.078658 |
| that | 2915 | 0.011510 | 6.440919 | 0.074138 |
| was | 2821 | 0.005235 | 7.577496 | 0.039671 |
| his | 2113 | 0.001396 | 9.484674 | 0.013239 |
| at | 2075 | 0.003140 | 8.314890 | 0.026111 |
| her | 1822 | 0.001115 | 9.808143 | 0.010941 |
| but | 1784 | 0.004786 | 7.706833 | 0.036888 |
| not | 1771 | 0.004831 | 7.693317 | 0.037170 |
| with | 1751 | 0.005283 | 7.564411 | 0.039963 |
| for | 1671 | 0.007596 | 7.040510 | 0.053481 |
| she | 1626 | 0.001006 | 9.956840 | 0.010019 |
With the spaCy probabilities, we can see that our entropy dropped significantly, from to . The reason is that probability distribution from the spaCy model has a significantly larger range, defined by the total vocabulary. The vocabulary from Crime and Punishment was 10,800 unique words, whereas the vocabulary in the en_core_web_md model is 710,657. As a result, each individual word has less information content, and smaller entropy contribution.
Let’s go back to a few interesting words for direct comparisons.
words_of_interest = ["the", "a", "crime", "punishment", "giantkiller", "fantasy"]pd.set_option('display.float_format', lambda x: '%.6f' % x)
print("\nInteresting word values with in-context probability:")full_text_words = ( crime_data['word_data'][crime_data['word_data']['word'] .isin(words_of_interest)] .sort_values("word"))display(full_text_words)
print("\nInteresting word values with spaCy probability:")full_text_words_spacy = ( crime_data_spacy['word_data'][crime_data_spacy['word_data']['word'] .isin(words_of_interest)] .sort_values("word"))display(full_text_words_spacy)Interesting word values with in-context probability:
| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| the | 7976 | 0.038645 | 4.693564 | 0.181384 |
| a | 4622 | 0.022394 | 5.480712 | 0.122738 |
| crime | 52 | 0.000252 | 11.954574 | 0.003012 |
| fantasy | 4 | 0.000019 | 15.655014 | 0.000303 |
| giantkiller | 1 | 0.000005 | 17.655014 | 0.000086 |
| punishment | 4 | 0.000019 | 15.655014 | 0.000303 |
Interesting word values with spaCy probability:
| word | frequency | probability | information | entropy_contribution |
|---|---|---|---|---|
| the | 7976 | 0.029341 | 5.090934 | 0.149374 |
| a | 4622 | 0.019648 | 5.669486 | 0.111393 |
| crime | 52 | 0.000050 | 14.293683 | 0.000712 |
| fantasy | 4 | 0.000027 | 15.179080 | 0.000409 |
| giantkiller | 1 | 0.000000 | 28.853901 | 0.000000 |
| punishment | 4 | 0.000020 | 15.626908 | 0.000309 |
Using the probabilities provided by spaCy, we can see significant changes compared to our vocab in Crime and Punishment alone. For example, the most common word from Crime and Punishment, the, went from a probability of to , and had a corresponding change in information up from to , but also a drop in entropy contribution from to .
Final Thoughts
Over the course of this discussion, we’ve learned a lot about entropy and information content. But, we’ve also left a lot out! The biggest omission is probably the question of using conditional probability in our calculations. As with letters, we know that words in a language follow certain patterns, meaning that given a particular word, or a particular set of words, the probability distribution changes for what word is most likely to come next. Of course, this is the whole problem being solved by large language models! That’s obviously a much bigger topic than we can cover here.
The important point to take away from this discussion is that entropy is one of many tools we can use to understand the complexity of a text. It tells us something not only about the information content of the text, but also about our efficiency and effectiveness as communicators. So, next time you’re evaluating a text, think about calculating its entropy!
