How Does a Computer Learn to Read?

Believe it or not, computers are illiterate. Despite appearances, a computer can’t “read” a word, understand it’s meaning, and place it in context next to adjacent words. To a computer, the words you read on the monitor are just a way of transmitting data to you. The computer itself is operating on a much lower level of abstraction, because it can only store information as bits—ones and zeros that must be strung together to represent something more complex.

Consider the letter a. A computer doesn’t have any way to store an a in memory, because computer memory is a string of switches that only have two states: on (1) or off (0). So, the computer has to find a way to represent the letter a with those switches. To solve this problem, humans have created various systems that match letters and symbols with decimal numbers. In ASCII for example, a is matched to 97. Now, instead of the realm of letters, we’re in the realm of numbers, and computers are great with numbers. A 97 can in turn be converted into binary format rather than decimal format, and we get 01100001, which can be represented by the aforementioned switches in computer memory. To humans, this means a, but as far as the computer is concerned, letters don’t exist.

Setting aside the intricacies of digital storage, let’s consider why this matters in text analytics. Although we’re not directly concerned with how computers store information, we are concerned with how we computers can understand and manipulate information. So, if we’re interested in statistical analysis, or building machine learning models, then we need a way to convert texts into numbers so that we can carry out mathematical operations on them.

It’s tempting to think, “Oh, great, we already have binary! We can just use that!” But there is a problem. As mentioned before, the computer doesn’t attach any meaning to 01100001. Moreover, a computer doesn’t attach meaning to a string of binary digits, that convert into letters, that then spell the word apple, or mountain, or any other word. In analytics, the meaning matters, so we’re going to have to find ways to convert text into numbers, which we can manipulate with math, but still maintain meaning. Let’s take a look at a few ways to do this.

Just a Bag-o-Words

At its most basic level, a text is a collection of words. We know of course that the order of words matters, but even without context, the types and frequencies of words used in a text carry meaning. If, for example, I told you that the most common non-stopwords in a text were ‘goal’, ‘player’, ‘score’, and ‘ball’, then you could reasonably guess that the text has to do with sports. Using these frequencies, we can represent a text with a bag-of-words (BOW), so-called because this approach is to simply take all the words, count their frequencies, and toss them into a single collection without order. We can do this by first creating a vocabulary for the text, and then counting the frequencies of each word in the vocabulary.

1
# utility
2
import re
3
from collections import Counter
4

5
# data manipulation
6
import pandas as pd
7
import numpy as np
8

9
# visualization
10
import matplotlib.pyplot as plt
11
import seaborn as sns
12

13
def get_words(text: str) -> list[str]:
14
    """
15
    Extracts words from a text string, converting to lowercase
16
    and removing non-alphabetic characters.
17

18
    Args:
19
        text (str): The text to extract words from
20

21
    Returns:
22
        list[str]: A list of words
23
    """
24
    text = re.sub(r"[^\w\s]", "", text)
25
    words = text.lower().split()
26
    return words
27

28
def get_vocab(text: str) -> list[str]:
29
    """
30
    Extracts unique words from a text string, converting to lowercase
31
    and removing non-alphabetic characters.
32

33
    Args:
34
        text (str): The text to extract words from
35

36
    Returns:
37
        list[str]: An alphabetical list of unique words
38
    """
39
    words = get_words(text)
40
    vocab = list(set(words))
41
    vocab = sorted(vocab)
42
    return vocab

In our first step to create a BOW, we’ll create a vocabulary. For the sake of simplicity, we’re going to remove punctuation and make all words lowercase. We’ll then represent the vocabulary as an alphabetically sorted list. The reason it is sorted is that we need to maintain word order to match with our frequency list.

1
animal_sentences = [
2
    "The cat licked his lips loudly, staring hungrily at the bird.",
3
    "The dog barked while the cat ate all the fish.",
4
    "The bird chirped loudly as the cat purred beside it.",
5
    "The bird on the fence watched the growling dog.",
6
    "With a swift leap, the cat landed from the wall."
7
]
8
animal_text = " ".join(animal_sentences)
9

10
animal_vocab = get_vocab(animal_text)
11
print("Length of animal_vocab:", len(animal_vocab))
12
print(animal_vocab)

Length of animal_vocab: 32
['a', 'all', 'as', 'at', 'ate', 'barked', 'beside', 'bird', 'cat', 'chirped', 'dog', 'fence', 'fish', 'from', 'growling', 'his', 'hungrily', 'it', 'landed', 'leap', 'licked', 'lips', 'loudly', 'on', 'purred', 'staring', 'swift', 'the', 'wall', 'watched', 'while', 'with']

Now that we have a sorted list of all the words in our sample sentences about animals, we can count frequencies for each of the words.

1
def get_word_frequencies(text: str, vocab: list[str]) -> list[int]:
2
    """
3
    Counts the frequency of each word in a text string.
4

5
    Args:
6
        text (str): The text to count word frequencies in
7
        vocab (list[str]): A list of unique words to count
8

9
    Returns:
10
        list[int]: A list of word frequencies
11
    """
12
    words = get_words(text)
13
    word_counts = Counter(words)
14
    frequencies = [word_counts[word] for word in vocab]
15
    return frequencies
16

17
animal_frequencies = get_word_frequencies(animal_text, animal_vocab)
18
print("Length of animal_frequencies:", len(animal_frequencies))
19
print(animal_frequencies)

Length of animal_frequencies: 32
[1, 1, 1, 1, 1, 1, 1, 3, 4, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 12, 1, 1, 1, 1]

Note that our animal_vocab and animal_frequencies are lists of the same length. This is important because we expect the frequencies to match to the corresponding item in the vocab. To check how often a particular word is used, we should make a few helpers that convert indices to words, and words to indices.

1
# string to index map
2
animal_stoi = {word: i for i, word in enumerate(animal_vocab)}
3

4
# index to string map
5
animal_itos = {i: word for i, word in enumerate(animal_vocab)}
6

7
print(f"Word at index 10: {animal_itos[10]}")
8
print(f"Index of word 'dog': {animal_stoi['dog']}")
9

10
# OUTPUT
11
# Word at index 10: dog
12
# Index of word 'dog': 10

Now that we have our maps, we can check the frequency of particular words.

1
word = "cat"
2
word_index = animal_stoi[word]
3
word_frequency = animal_frequencies[word_index]
4
print(f"Frequency of '{word}' (index: {word_index}): {word_frequency}")
5

6
# OUTPUT
7
# Frequency of 'cat' (index: 8): 4

In this approach, we have stored our vocabulary and frequencies separately. We’ve done this for reasons that will soon become clear as we compare different text representations, but more typically we would represent a BOW as a dictionary.

1
animal_bow = {word: freq for word, freq in zip(animal_vocab, animal_frequencies)}
2
print("Length of animal_bow:", len(animal_bow))
3
print(animal_bow)

Length of animal_bow: 32
{'a': 1, 'all': 1, 'as': 1, 'at': 1, 'ate': 1, 'barked': 1, 'beside': 1, 'bird': 3, 'cat': 4, 'chirped': 1, 'dog': 2, 'fence': 1, 'fish': 1, 'from': 1, 'growling': 1, 'his': 1, 'hungrily': 1, 'it': 1, 'landed': 1, 'leap': 1, 'licked': 1, 'lips': 1, 'loudly': 2, 'on': 1, 'purred': 1, 'staring': 1, 'swift': 1, 'the': 12, 'wall': 1, 'watched': 1, 'while': 1, 'with': 1}

Aside from identifying word frequencies (which is certainly useful in its own right), what can we do with a BOW? Well, for starters, we can compare texts by preparing counts for all of the documents and arranging them in a single matrix. This is known as a term-document matrix (TDM).

1
def get_tdm(texts: list[str], vocab: list[str]) -> np.ndarray:
2
    """
3
    Creates a term-document matrix from a list of text strings.
4

5
    Args:
6
        texts (list[str]): A list of text strings
7
        vocab (list[str]): A list of unique words
8

9
    Returns:
10
        np.ndarray: A term-document matrix
11
    """
12
    # start with a matrix of all zeros where columns are words
13
    # in the shared vocab, and rows are documents
14
    tdm = np.zeros((len(texts), len(vocab)), dtype=int)
15

16
    # get the word frequencies for individual texts and store
17
    # them in the matrix
18
    for i, text in enumerate(texts):
19
        frequencies = get_word_frequencies(text, vocab)
20
        tdm[i] = frequencies
21
    return tdm
22

23
animal_tdm = get_tdm(animal_sentences, animal_vocab)
24
print("Shape of animal_tdm:", animal_tdm.shape)
25
print(animal_tdm)

Shape of animal_tdm: (5, 32)
[[0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 2 0 0 0 0]
 [0 1 0 0 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 1 0]
 [0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 2 0 0 0 0]
 [0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 3 0 1 0 0]
 [1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 2 1 0 0 1]]

1
# test that the column sums (total word counts across all documents)
2
# match the word frequencies in the vocabulary
3
column_sums = np.sum(animal_tdm, axis=0)
4
match = np.array_equal(column_sums, animal_frequencies)
5

6
print("Column sums match frequencies:", match)
7

8
# OUTPUT
9
# Column sums match frequencies: True

With our TDM, we can now do all sorts of interesting statistical comparisons, but perhaps most importantly, we can use the documents as inputs to train machine learning models. Imagine we had some label for each sentence, like [1, 0, 0, 1, 1] where 0 means “Class A” and 1 means “Class B”. Having a numerical representation of each document with a known label would allow us to train a model to classify documents. We won’t get into the details of training a model here, but you can see why the numerical representation matters—without it, we wouldn’t have anything to feed into the model, since models can only operate on numerical representations of text.

The BOW and TDM approach certainly has value, but we’re missing something important: word order. We know that word order is critical to language, and using a BOW loses that meaning. Let’s consider some ways to represent our text numerically without losing word order.

It’s Getting Hot in Here…

One approach to representing a text numerically without losing the information we get from word order is one-hot encoding. In this scheme, we represent each word as an array of numbers equal to the length of the vocabulary, where every number is zero except the index of the word.

1
def get_one_hot_vocab(vocab: list[str]) -> np.ndarray:
2
    """
3
    Creates a one-hot encoding matrix from a list of unique words.
4

5
    Args:
6
        vocab (list[str]): A list of unique words
7

8
    Returns:
9
        np.ndarray: A one-hot encoding matrix
10
    """
11
    vocab_size = len(vocab)
12
    one_hot_vocab = np.eye(vocab_size)
13
    return one_hot_vocab
14

15
animal_one_hot_vocab = get_one_hot_vocab(animal_vocab)
16

17
print("Shape of animal_one_hot_vocab:", animal_one_hot_vocab.shape)
18
animal_one_hot_vocab

array([[1., 0., 0., ..., 0., 0., 0.],
       [0., 1., 0., ..., 0., 0., 0.],
       [0., 0., 1., ..., 0., 0., 0.],
       ...,
       [0., 0., 0., ..., 1., 0., 0.],
       [0., 0., 0., ..., 0., 1., 0.],
       [0., 0., 0., ..., 0., 0., 1.]], shape=(32, 32))

Here, we see the one-hot vocabulary, which matches up by index with our word vocabulary. Each row in the one-hot vocabulary consists of all zeros, except for a one in the column corresponding to the word index. We can see this below, with the first two words from the vocabulary. Notice how the 1 moves one spot to the right with each item.

1
for i, word in enumerate(animal_vocab[:3]):
2
    print(f"One-hot encoding for '{word}':")
3
    print(animal_one_hot_vocab[i])
4
    print()

One-hot encoding for 'a':
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.]

One-hot encoding for 'all':
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.]

One-hot encoding for 'as':
[0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.]

Now that we have our one-hot vocabulary, we can use it to create a one-hot matrix (OHM) for our text as a whole.

1
def get_one_hot_matrix(text: str, vocab: list[str]) -> np.ndarray:
2
    """
3
    Encodes a text string using one-hot encoding.
4

5
    Args:
6
        text (str): The text to encode
7
        vocab (list[str]): A list of unique words
8

9
    Returns:
10
        np.ndarray: A one-hot encoded matrix
11
    """
12
    one_hot_vocab = get_one_hot_vocab(vocab)
13
    stoi = {word: i for i, word in enumerate(vocab)}
14

15
    words = get_words(text)
16
    word_indices = [stoi[word] for word in words]
17

18
    return one_hot_vocab[word_indices]
19

20
def one_hot_to_word(one_hot_row: np.ndarray, vocab: list[str]) -> str:
21
    """
22
    Converts a one-hot encoded row back to a word.
23

24
    Args:
25
        one_hot_row (np.ndarray): A one-hot encoded row
26
        vocab (list[str]): A list of unique words
27

28
    Returns:
29
        str: The word corresponding to the one-hot row
30
    """
31
    itos = {i: word for i, word in enumerate(vocab)}
32
    word_index = np.argmax(one_hot_row)
33
    return itos[word_index]
34

35
animal_one_hot_matrix = get_one_hot_matrix(animal_text, animal_vocab)
36
print("Shape of animal_one_hot_matrix:", animal_one_hot_matrix.shape)
37
print(animal_one_hot_matrix)

Shape of animal_one_hot_matrix: (50, 32)
[[0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]]

Looking at the shape of our one-hot matrix (OHM) for the animal text, we see that it is (50, 32), meaning 50 rows by 32 columns. This is exactly what we expect, given that there are 50 total words in the text, and 32 unique vocabulary words. We can confirm that our OHM is correct by checking if the rows of the OHM have the 1 in the same index as the word’s vocab index.

1
for word_idx, word in enumerate(get_words(animal_text)[:5]):
2
    vocab_idx = animal_stoi[word]
3
    row = animal_one_hot_matrix[word_idx]
4
    one_idx = np.argmax(row)
5

6
    print(f"{word} ({vocab_idx}) ->")
7
    print(f"{row} ->")
8
    print(f"{one_idx} == {vocab_idx}")
9
    print("")

the (27) ->
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 1. 0. 0. 0. 0.] ->
27 == 27

cat (8) ->
[0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.] ->
8 == 8

licked (20) ->
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.] ->
20 == 20

his (15) ->
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.] ->
15 == 15

lips (21) ->
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.] ->
21 == 21

As with our BOW approach, we could now use OHM representations to feed texts into a machine learning model. But unlike the BOW, the OHM representation preserves word order, and the associated information that comes with the patterns in that order. We’ll leave implementation of that to another time, because now we have yet another problem! Although we have gained some information by preserving word order, we still don’t have any information about the meaning of the words. For that, we’re going to have to turn to one of the most important tools in machine learning and text analytics: embeddings.

Embedding Linguistic Meaning in Numbers

To say that embeddings have revolutionized machine learning is an understatement. Along with transformers, embeddings are arguably one of the most important ideas that led to the dramatic progress we have seen in machine learning and deep learning. The reason is that embeddings give us more than just abstract representations of text; they can also give us contextual meaning. To get an idea of what that means, let’s explore two types of embeddings: random embeddings, and contextual embeddings.

First off, what is a text embedding? In short, it’s a vector of numbers that represents a word. In a similar fashion to one-hot encoding, we can create an embedding by iterating over the vocabulary of a text and generating a vector to represent each word. However, unlike the one-hot encoding approach where the vector was all zeros, except for a one at the index of the word, in the embedding approach the numbers are all decimals (aka floats). Let’s start out by creating some random embeddings.

1
def create_word_embeddings(
2
        vocab: list[str], embedding_dim: int = 3, seed: int = 42
3
    ) -> dict[str, np.ndarray]:
4
    """
5
    Create word embeddings for a vocabulary.
6

7
    Args:
8
        vocab (list[str]): List of words in the vocabulary
9
        embedding_dim (int, optional): Dimension of the embedding vectors. Defaults to 3.
10
        seed (int, optional): Random seed for reproducibility. Defaults to 42.
11

12
    Returns:
13
        dict[str, np.ndarray]: Dictionary mapping words to their embedding vectors
14
    """
15
    np.random.seed(seed)
16
    embeddings = np.array([np.random.normal(0, 0.1, (embedding_dim,)) for word in vocab])
17

18
    return embeddings
19

20
animal_word_embeddings = create_word_embeddings(animal_vocab)
21

22
print("Shape of animal_word_embeddings:", animal_word_embeddings.shape)
23

24
# OUTPUT
25
# Shape of animal_word_embeddings: (32, 3)

As with our one-hot vocabulary, our embeddings vocabulary has 32 rows, one for each word in the word vocabulary. The number of columns though differs. In our example, we have just three columns, or three dimensions in our embeddings. We might just as easily increased this to 10, or 50, or 100,000 dimensions. The more dimensions, the more fine grained the representation, but it comes at a cost of efficiency and size. In practice, major language models have thousands of embeddings.

Earlier, I said that embeddings are advantageous because they can approximate meaning (at least in a vague sense). To understand what this means, we’ll look at a few sample words, and then come back to them when we use our contextual embeddings.

1
cat_embedding = animal_word_embeddings[animal_stoi["cat"]]
2
dog_embedding = animal_word_embeddings[animal_stoi["dog"]]
3

4
print("Embedding for 'cat':", cat_embedding)
5
print("Embedding for 'dog':", dog_embedding)

Embedding for 'cat': [-0.05443827  0.01109226 -0.11509936]
Embedding for 'dog': [-0.06017066  0.18522782 -0.00134972]

Above are the embeddings for ‘cat’ and ‘dog’. They’re different (as expected), but do they have meaning beyond being unique? One of the amazing things about embeddings is that we can calculate the distance between them, which actually lets us measure whether they are related. We do this using a method called cosine similarity, which is a linear algebra operation that takes two vectors $A$ and $B$ (like our embeddings) and returns a value in the range $[-1, 1]$ . For the sake of simplicity, we’ll leave a full explanation for another time, but the important thing to know is that a value of $-1$ indicates exact opposites, a value of $0$ means the vectors are orthogonal (no relation), and a value of $1$ means they’re exactly the same.

\cos(\theta) = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|}

Now, we can use cosine similarity to measure the distance between or dog and cat embeddings.

1
def cosine_similarity(v1: np.ndarray, v2: np.ndarray) -> float:
2
    """
3
    Calculate the cosine similarity between two vectors.
4

5
    Args:
6
        v1 (np.ndarray): First vector
7
        v2 (np.ndarray): Second vector
8

9
    Returns:
10
        float: Cosine similarity between the vectors (-1 to 1)
11
    """
12
    # Calculate dot product
13
    dot_product = np.dot(v1, v2)
14

15
    # Calculate magnitudes
16
    norm_v1 = np.linalg.norm(v1)
17
    norm_v2 = np.linalg.norm(v2)
18

19
    # Calculate cosine similarity
20
    similarity = dot_product / (norm_v1 * norm_v2)
21

22
    return similarity
23

24
cat_dog_similarity = cosine_similarity(cat_embedding, dog_embedding)
25
print("Cosine similarity between 'cat' and 'dog':", cat_dog_similarity)
26

27
# OUTPUT
28
# Cosine similarity between 'cat' and 'dog': 0.22037684515784212

For our random embeddings, we have a cosine similarity of 0.22037 for the words ‘cat’ and ‘dog’, suggesting a mild measure of relation. Is this what we expect? In the popular imagination, dogs and cats are of course opposites, but when you think about it, they’re actually very similar. Both are mammals, both have four legs, both have fur, and both are human companions. Given as much, a mild relationship doesn’t quite seem right. But, since our embeddings are random, this result is also random. (With a different seed, we would get something totally different!) In other words, the embeddings have no meaning whatsoever, other than differentiating between words.

Before moving on, let’s go ahead and convert our full text to embeddings, and see what comes out.

1
def text_to_embeddings(text: str, vocab: list[str], embeddings: np.ndarray) -> np.ndarray:
2
    """
3
    Convert text to sequence of word embeddings.
4

5
    Args:
6
        text (str): Input text
7
        vocab (list[str]): List of vocabulary words
8
        embeddings (np.ndarray): Array of word embeddings
9

10
    Returns:
11
        np.ndarray: Array of word embeddings for the text
12
    """
13
    words = get_words(text)
14

15
    # Get word to index mapping
16
    stoi = {word: i for i, word in enumerate(vocab)}
17

18
    # Get embedding for each word
19
    text_embeddings = []
20
    for word in words:
21
        word_idx = stoi[word]
22
        text_embeddings.append(embeddings[word_idx])
23

24
    return np.array(text_embeddings)
25

26
word_embeddings = create_word_embeddings(animal_vocab)
27
animal_text_embeddings = text_to_embeddings(animal_text, animal_vocab, word_embeddings)
28
print("Shape of animal_text_embeddings:", animal_text_embeddings.shape)
29
print(animal_text_embeddings)
30
print()

Shape of animal_text_embeddings: (50, 3)
[[ 0.03571126  0.1477894  -0.05182702]
 [-0.05443827  0.01109226 -0.11509936]
 [-0.04791742 -0.0185659  -0.1106335 ]
 [-0.07198442 -0.04606388  0.10571222]
 [-0.11962066  0.08125258  0.135624  ]
 [-0.00720101  0.10035329  0.0361636 ]
 [ 0.08219025  0.00870471 -0.02990074]
...
 [ 0.01968612  0.07384666  0.01713683]
 [ 0.03571126  0.1477894  -0.05182702]
 [-0.08084936 -0.0501757   0.09154021]]

Great! now we have a matrix of embeddings that represents our text, and as with our other text representation models, we could use embeddings like this to train machine learning models on tasks like classification. Now, the models likely wouldn’t be very good, as the embeddings are random, but as with the one-hot encoding matrix, they preserve word order, which is something! To really get the most out of embeddings, we need to give them meaning.

Adding Context to Embeddings

The obvious first question is, how do we give embeddings meaning? The answer is more complicated than we can cover in this article, but the quick version is as follows. First, we take random embeddings like the ones we created before. And then, we use them to train an embedding model, usually on a task like predicting words. On each training cycle, the model updates the weights—that is, the decimal numbers inside our embeddings. Over time, as those weights are updated, they start to acquire meaning beyond just being unique as compared with other words. We can see this by using the same cosine similarity function we looked at before.

In our example, we’ll use pre-trained BERT embeddings, but there are lots of other options, like GPT, FastText, and more. The important thing is that these are not random embeddings, but contextual embeddings that have been trained in a way that gives them meaning.

1
from transformers import AutoTokenizer, AutoModel
2
import torch
3

4
def get_contextual_embeddings(
5
    text: str,
6
    model: torch.nn.Module,
7
    tokenizer: AutoTokenizer,
8
    device: torch.device,
9
    vocab: list[str] = None,
10
) -> dict[str, torch.Tensor]:
11
    """
12
    Get contextual embeddings for text.
13

14
    Args:
15
        text (str): Input text
16
        model (torch.nn.Module): Pretrained model
17
        tokenizer (AutoTokenizer): tokenizer
18
        device (torch.device): Device to run the model on
19
        vocab (list[str], optional): List of words to create embeddings for.
20
                                   If None, returns raw embeddings.
21

22
    Returns:
23
        dict[str, torch.Tensor]: Dictionary mapping words to their embeddings if vocab provided,
24
                                otherwise returns raw embeddings
25
    """
26
    inputs = tokenizer(text, return_tensors="pt", padding=True, truncation=True)
27
    inputs = {k: v.to(device) for k, v in inputs.items()}
28

29
    with torch.no_grad():
30
        outputs = model(**inputs)
31
    embeddings = outputs.last_hidden_state
32

33
    if vocab is None:
34
        return embeddings
35

36
    embedding_map = {}
37
    tokens = tokenizer.convert_ids_to_tokens(inputs['input_ids'][0])
38

39
    for word in vocab:
40
        word_tokens = tokenizer(word, return_tensors="pt")['input_ids'][0][1:-1].to(device)
41
        word_embeddings = []
42

43
        for i in range(len(tokens)):
44
            if tokens[i] == tokenizer.convert_ids_to_tokens(word_tokens.cpu())[0]:
45
                word_embeddings.append(embeddings[0, i].cpu())
46

47
        if word_embeddings:
48
            embedding_map[word] = torch.stack(word_embeddings).mean(0)
49

50
    return np.array(list(embedding_map.values()))
51

52
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
53
bert_tokenizer = AutoTokenizer.from_pretrained("bert-base-uncased")
54
bert_model = AutoModel.from_pretrained("bert-base-uncased").to(device)
55

56
contextual_word_embeddings = get_contextual_embeddings(
57
    animal_text,
58
    model=bert_model,
59
    tokenizer=bert_tokenizer,
60
    device=device,
61
    vocab=animal_vocab
62
)
63

64
print(contextual_word_embeddings.shape)
65

66
# OUTPUT
67
# (32, 768)

One thing to notice in our contextual embeddings is just how big they are! Each embedding has 768 dimensions, which as you can imagine, requires a very big model when you are talking about every word in a language (rather than just our small vocabulary of 32 words in our animal texts). Now, let’s compare these embeddings on the same words, ‘cat’ and ‘dog’, as we did with our random embeddings.

1
cat_contextual_embedding = contextual_word_embeddings[animal_stoi["cat"]]
2
dog_contextual_embedding = contextual_word_embeddings[animal_stoi["dog"]]
3

4
cat_dog_contextual_similarity = cosine_similarity(
5
    cat_contextual_embedding,
6
    dog_contextual_embedding
7
)
8

9
print("Cosine similarity for words 'cat' and 'dog':")
10
print("Random embeddings:", cat_dog_similarity)
11
print("Contextual embeddings:", cat_dog_contextual_similarity)

Cosine similarity for words 'cat' and 'dog':
Random embeddings: 0.22037684515784212
Contextual embeddings: 0.86056995

Huge difference! As we discussed before, if the embeddings have meaning, we would expect ‘cat’ and ‘dog’ to be pretty similar, and indeed, with the BERT embeddings they have a cosine similarity of 0.8605. Pretty darn close! Of course, as we said, our random embeddings could have shown closer similarity if the random rolls had turned out differently. Let’s try a few other word pairs to confirm that the contextual embeddings really do have more meaning.

1
word_pairs = [
2
    ("cat", "dog"),
3
    ("cat", "bird"),
4
    ("cat", "fish"),
5
    ("cat", "wall"),
6
    ("wall", "fence"),
7
]
8

9
similarities = []
10
for w1, w2 in word_pairs:
11
    idx1, idx2 = animal_stoi[w1], animal_stoi[w2]
12

13
    emb1, emb2 = animal_word_embeddings[idx1], animal_word_embeddings[idx2]
14
    sim1 = cosine_similarity(emb1, emb2)
15

16
    emb1, emb2 = contextual_word_embeddings[idx1], contextual_word_embeddings[idx2]
17
    sim2 = cosine_similarity(emb1, emb2)
18

19
    similarities.append({
20
        'word 1': w1,
21
        'word 2': w2,
22
        'random similarity': sim1,
23
        'contextual similarity': sim2
24
    })
25

26
df_similarities = pd.DataFrame(similarities)
27
display(df_similarities)

word 1	word 2	random similarity	contextual similarity
cat	dog	0.220377	0.860570
cat	bird	0.959157	0.766288
cat	fish	0.394307	0.400762
cat	wall	-0.396528	0.391683
wall	fence	-0.282078	0.697818

As we look at multiple word pairs, it becomes clear that contextual embeddings are working as expected. With our random embeddings, the similarity is… well.. random. But with the contextual embeddings we seem to have real meaning. The word ‘cat’ is very similar to ‘dog’ (both are mammals, furry, household pets), ‘cat’ is less similar to ‘bird’, even less similar to ‘fish’, and not really similar at all to ‘wall’. However, ‘wall’ is quite similar to ‘fence’. All of this falls within our expectations, and shows the power of contextual embeddings. To illustrate even further, we can plot our two sets of embeddings using a technique called dimensionality reduction, which let’s us plot multi-dimensional vectors (like our embeddings) on a two-dimensional canvas. (We’ll ignore the details of dimensionality reduction for now, but it’s worth looking into if you’re interested!)

1
from sklearn.decomposition import PCA
2

3
def plot_embeddings(embeddings: np.ndarray, vocab: list[str], highlight_words: list[dict],
4
                   figsize: tuple=(10, 8), title: str="Word Embeddings Visualization") -> None:
5
    """
6
    Plots word embeddings in 2D space with highlighted word groups.
7

8
    Args:
9
        embeddings (np.ndarray): Matrix of word embeddings
10
        vocab (list[str]): List of words corresponding to embeddings
11
        highlight_words (list[dict]): List of dictionaries with 'title' and 'words' keys
12
                                    for highlighting word groups
13
        figsize (tuple): Figure size (width, height)
14
        title (str): Plot title. Defaults to "Word Embeddings Visualization"
15
    """
16
    pca = PCA(n_components=2)
17
    embeddings_2d = pca.fit_transform(embeddings)
18
    df = pd.DataFrame({
19
        'PC1': embeddings_2d[:, 0],
20
        'PC2': embeddings_2d[:, 1],
21
        'word': vocab
22
    })
23

24
    plt.figure(figsize=figsize)
25

26
    highlighted = set(word for group in highlight_words for word in group['words'])
27
    regular_words = [w for w in vocab if w not in highlighted]
28
    regular_mask = df['word'].isin(regular_words)
29
    sns.scatterplot(data=df[regular_mask], x='PC1', y='PC2', alpha=0.6, color='gray')
30

31
    colors = sns.color_palette('bright', n_colors=len(highlight_words))
32
    for group, color in zip(highlight_words, colors):
33
        mask = df['word'].isin(group['words'])
34
        sns.scatterplot(data=df[mask], x='PC1', y='PC2', alpha=0.8,
35
                       color=color, label=group['title'])
36

37
    for idx, row in df.iterrows():
38
        plt.annotate(row['word'], (row['PC1'], row['PC2']),
39
                    xytext=(5, 5), textcoords='offset points')
40

41
    plt.title(title)
42
    plt.legend()
43
    plt.tight_layout()
44

45
animal_text_contextual_embeddings = text_to_embeddings(
46
    animal_text,
47
    animal_vocab,
48
    contextual_word_embeddings
49
)
50

51
print("Shape of animal_text_contextual_embeddings:", animal_text_contextual_embeddings.shape)

Shape of animal_text_contextual_embeddings: (50, 768)

First, let’s plot the random embeddings, highlighting a few words that we expect to be similar.

1
animal_words = ['dog', 'fish', 'bird', 'cat']
2
structure_words = ['fence', 'wall']
3
action_words = ['barked', 'purred', 'licked', 'growling', 'staring', 'chirped', 'landed']
4

5
highlight_words= [
6
    {'title': 'Animals', 'words': animal_words},
7
    {'title': 'Locations', 'words': structure_words},
8
    {'title': 'Actions', 'words': action_words}
9
]
10

11
plot_embeddings(
12
    word_embeddings,
13
    animal_vocab,
14
    highlight_words=highlight_words,
15
    title="Random Word Embeddings Visualization"
16

17
)

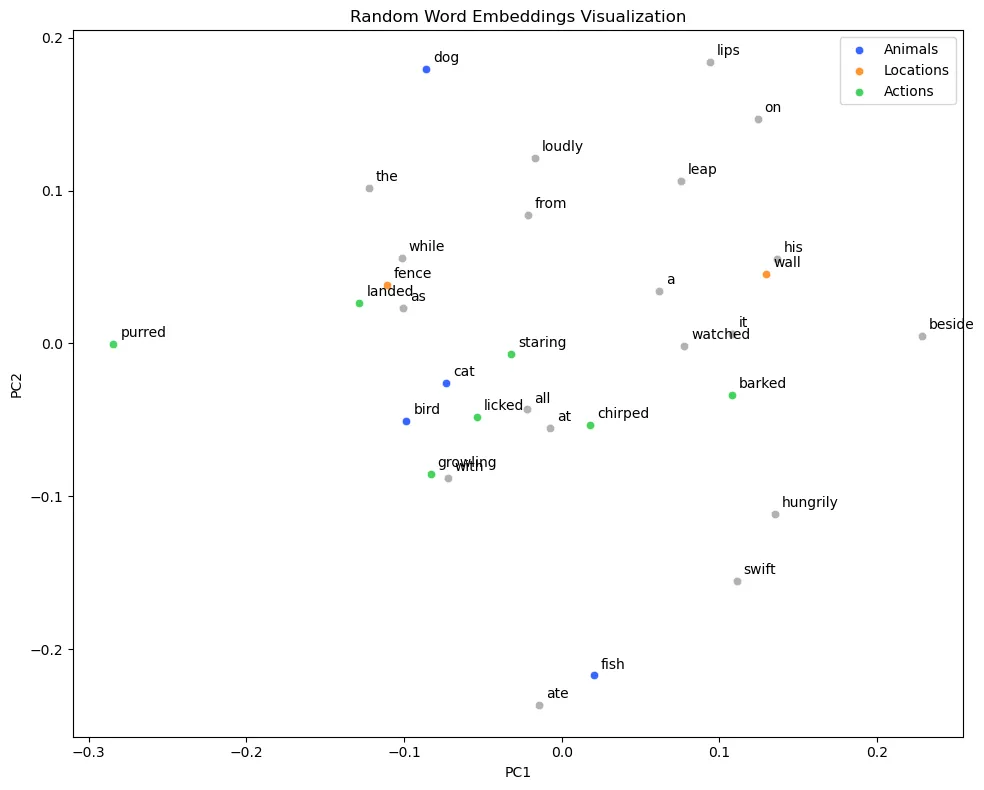
Bar chart of information content per letter.

In the plot of random word embeddings, the pattern seems essentially random (per expectations). Compare this to the plot of contextual embeddings.

1
plot_embeddings(
2
    contextual_word_embeddings,
3
    animal_vocab,
4
    highlight_words=highlight_words,
5
    title="Contextual Word Embeddings Visualization"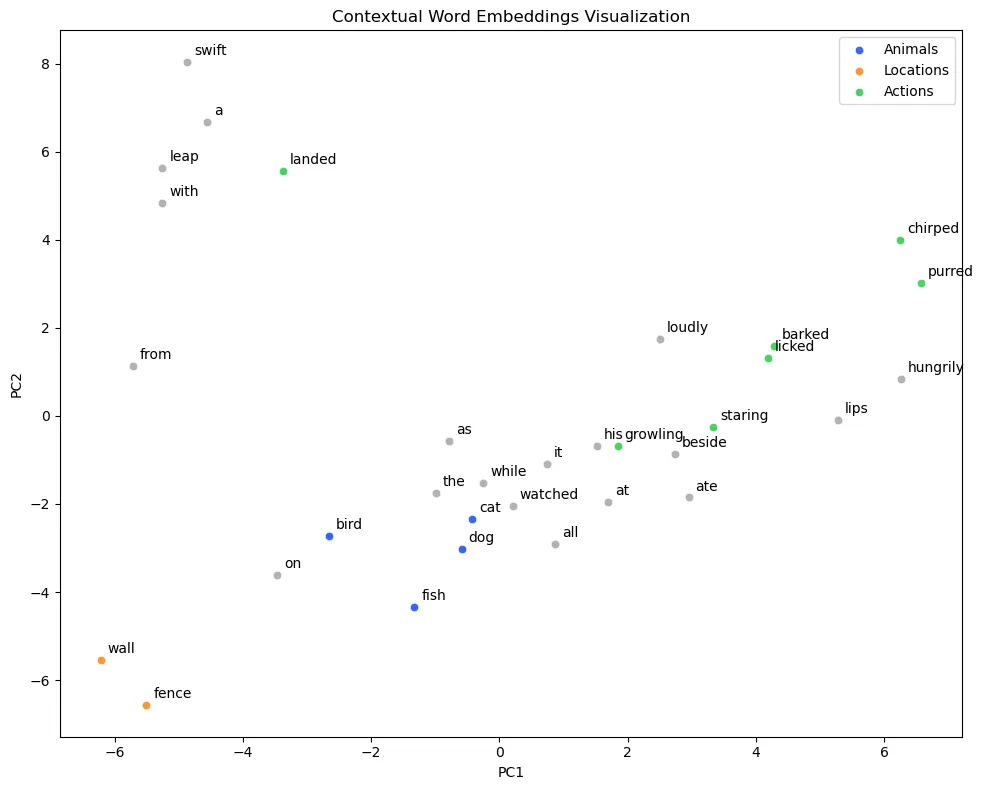
6
)

Bar chart of information content per letter.

As expected from our cosine similarity calculations, here we see a much clearer pattern. The points for ‘dog’ and ‘cat are directly next to one another, as are ‘wall’ and ‘fence’. It’s not a perfect system, but when we’re trying to convert the meaning we find in words into a format a computer can process, it’s pretty darn neat!

Is the Computer Literate Now?

Converting text representations into numbers clearly has huge benefits. The computer can now process them, run mathematical calculations, build models, etc. All things that weren’t possible with pure text. But is the computer literate? At some point, we leave the realm of computer science and enter the realm of philosophy. The computer still doesn’t understand the meaning in our texts, but it can recognize and predict patterns. In some ways, perhaps pattern recognition and “knowledge” aren’t all that different. Does the human brain, after all, not do the same thing? At some point, the distinction between how computers understand information, and how humans do, will become irrelevant. For our purposes in text analytics though, we can at least say that having ways of representing text as numbers gives us new and powerful tools.